La méthode de la variation de la constante sert à trouver une solution particulière à une équation différentielle linéaire du premier ordre après avoir calculé les solutions de l'équation homogène associée. Elle se termine toujours par un calcul de primitives.

La méthode avec un exemple

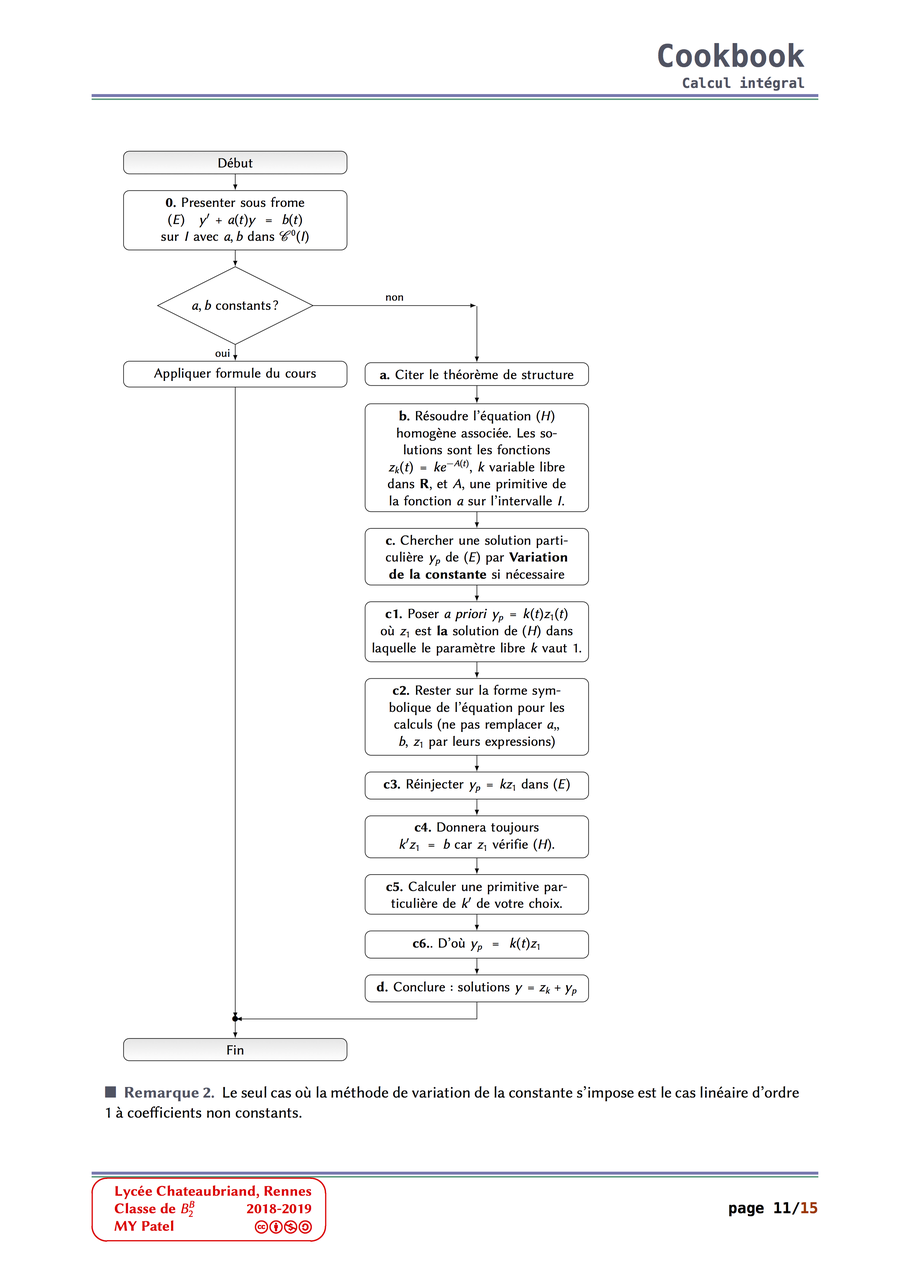
À vous de jouer

Résoudre les équations différentielles suivantes sur l'intervalle $I$ donné :

1. $I = \mathbf{R} \quad y'-2xy = x$
2. $I= ]-1;+\infty[ \quad y'+\dfrac{x}{x+1} y = x+1$
3. $I= \mathbf{R} \quad y'-y = x^{k}e^{x}$, où $k$ est un entier naturel fixé.